Why Randomized Optimization Needs Quantum Computing

Randomized optimization algorithms like Genetic Algorithms (GA), Simulated Annealing (SA), and Randomized Hill Climbing (RHC) are powerful tools for solving problems where traditional gradient-based methods fail. These “black-box” problems are common in fields like logistics, engineering design, and machine learning, where the optimization landscape is complex, non-differentiable, or riddled with local minima.

Our work, “Benchmarking Randomized Optimization Algorithms,” systematically evaluated these algorithms and highlighted a fundamental trade-off: effectiveness versus efficiency. While sophisticated algorithms like GA and MIMIC excel at finding high-quality solutions, they do so by exploring vast search spaces, which is incredibly computationally expensive. Simpler methods like RHC are faster but often get trapped in suboptimal solutions. This core limitation, the sheer computational cost of exploration, has often relegated these powerful methods to a niche.

However, the emergence of quantum computing promises to shatter this barrier, potentially making randomized search a practical, front-line tool for solving intractable problems.

The Bottleneck is in Searching the Landscape

The core challenge for any randomized optimization algorithm is to effectively balance exploration (searching broadly for new solution areas) and exploitation (honing in on the best-known solution).

As our paper shows, algorithms that heavily favor exploration, like Genetic Algorithms with large populations, perform well on complex “combinatorial” problems. They maintain a diverse set of potential solutions, cross-breeding them to navigate rugged landscapes. But this comes at a cost: evaluating and managing this population over many generations is slow. On the other hand, algorithms that favor exploitation, like a simple Randomized Hill Climber, quickly find the nearest peak but have no effective mechanism to escape it and find a potentially much higher peak elsewhere.

This is the classical bottleneck: exploring a vast problem space one step, or one population, at a time is often too slow to be practical.

[Figure 1] How more effective algorithms like GA and MIMIC consistently outperform simpler ones like RHC, but require more computational resources.

Quantum Superposition: Parallel Exploration on a Massive Scale

Quantum computing’s power lies in its fundamentally different approach to processing information. A classical bit is either a 0 or a 1. A quantum bit, or qubit, can exist in a superposition of both states simultaneously. We can represent the state of a qubit, $|\psi\rangle$, as a linear combination of the classical states $|0\rangle$ and $|1\rangle$:

Here, $\alpha$ and $\beta$ are complex numbers called probability amplitudes, and the probability of measuring the qubit as 0 is $|\alpha|^2$, while the probability of measuring it as 1 is $|\beta|^2$ (where $|\alpha|^2 + |\beta|^2 = 1$).

This concept becomes exponentially more powerful when we use multiple qubits. By extension, a register of $N$ qubits can represent every possible combination of $N$ bits, all $2^N$ classical states, at the same time. This is formally written as:

This is where the game changes for randomized search. Instead of a classical Genetic Algorithm that maintains a population of, say, 200 candidate solutions, a quantum computer could use a single quantum state $|\Psi\rangle$ to represent a superposition of millions or billions of candidate solutions simultaneously. Each $|i\rangle$ could encode a potential solution, and its coefficient $c_i$ would represent its amplitude in the mix.

Quantum operators could then act on this entire super-population in a single step.

Quantum Tunneling

Another powerful quantum phenomenon is tunneling. In classical optimization, if a solution is in a local minimum, it needs enough energy (or in the case of Simulated Annealing, a high enough “temperature”) to jump over a barrier to find a better minimum. If the barrier is too high, the algorithm gets stuck.

A quantum system, however, can tunnel directly through the barrier, even if it doesn’t have the energy to go over it. This is the principle behind Quantum Annealing, the quantum counterpart to Simulated Annealing.

This ability to tunnel provides a powerful new way to escape local minima. For optimization landscapes with tall, thin barriers separating a good solution from a great one, a quantum annealer could find the global minimum exponentially faster than its classical equivalent. This directly addresses the primary weakness of algorithms like RHC and SA, giving them a physical mechanism to avoid getting trapped.

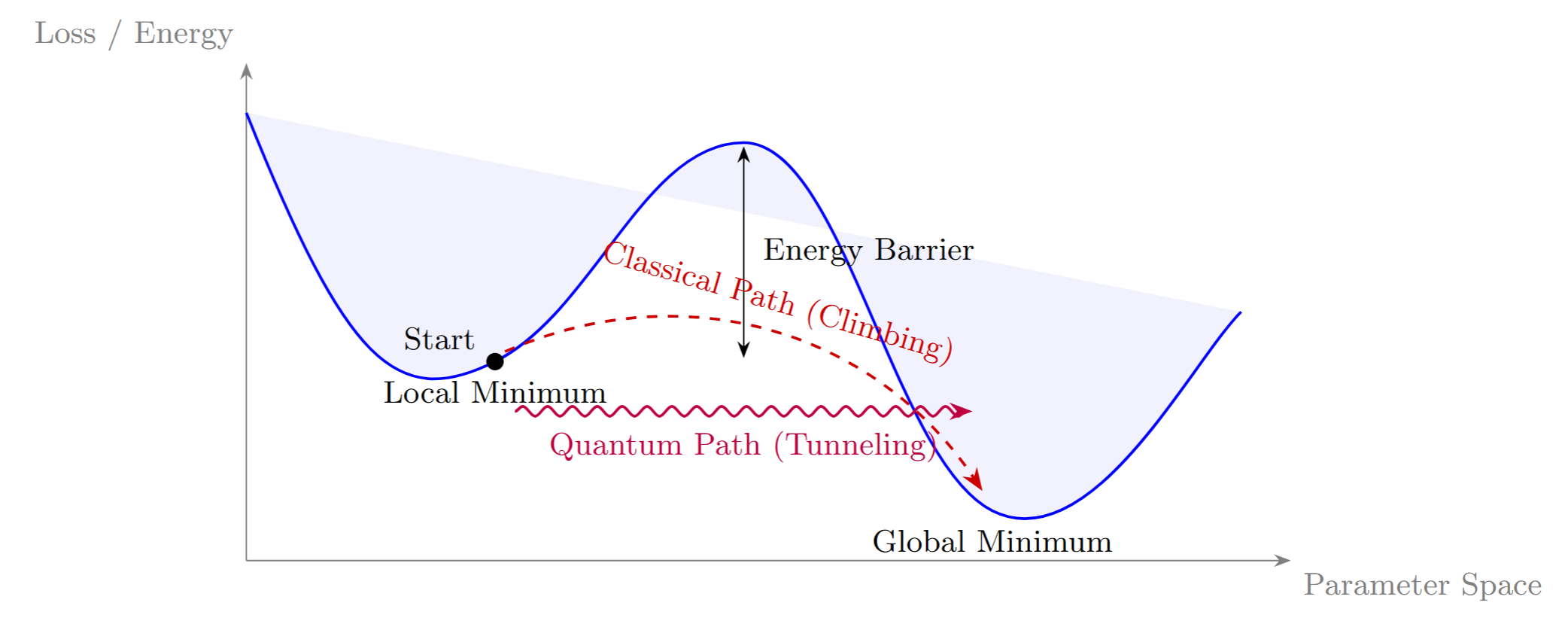[Figure 2] While a classical algorithm must climb over a barrier to escape a local minimum, a quantum algorithm can “tunnel” through it, finding a better solution more efficiently.

Conclusion

Randomized optimization algorithms are great in theory, but often stymied by the practical limits of classical computation. The very thing that makes them effective, their ability to perform a broad, unguided search, is also their biggest weakness.

Quantum computing directly addresses this bottleneck.

1. Superposition enables massively parallel exploration, turning the slow, iterative search of algorithms like GA into a highly efficient process.
2. Tunneling provides a physical shortcut to escape local minima, empowering simpler algorithms and making the search for the true global minimum far more robust.

While large-scale, fault-tolerant quantum computers are still on the horizon, the journey towards building them is marked by significant engineering milestones. For instance, recent work from Google on their Willow quantum chip is pushing the boundaries of quantum error correction, a critical step needed to build the stable, logical qubits required for practical computation [1].

References

[1] Google. “Meet Willow, our state-of-the-art quantum chip” Google AI Blog. https://blog.google/technology/research/google-willow-quantum-chip/